.jpg)
Disclaimer: Copyright infringement not intended.Out of the numerous factors that affect wind motion, the following are considered to be the most important:
(1) Horizontal pressure – gradient,
(2) Rotation of the earth (the Coriolis Force),
(3) Frictional forces,
(4) Centrifugal action of wind.
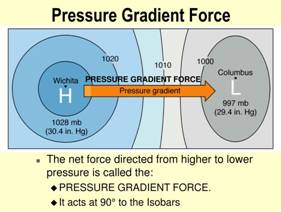The force that causes wind movement results from horizontal pressure difference. It is the direction and magnitude of the pressure gradient which ultimately determines wind direction and its velocity.
Wind moves from higher pressure to lower pressure. Thus, pressure differences cause the wind to blow, and the greater these differences, the greater the wind velocity. In other words, the interrelationship between gradient force and wind can be seen in the form of wind direction and wind-speed.
Since the direction of wind motion is always from higher pressure towards lower pressure, the line showing the direction of wind is always perpendicular to the isobars.
When the pressure gradient is steep, the wind velocity is higher, while the weak pressure gradient causes the wind to blow at a low speed. The spacing of the isobars is a measure of the amount of pressure change occurring over a given distance.
The same is expressed as the pressure gradient. Pressure gradient is steep, when the rate of change is great, while it is said to be weak when the rate of change is small. Therefore the velocity of wind can be estimated from the spacing of isobars.
Closely spaced isobars mean a steep pressure gradient and high velocity winds; widely spaced isobars, on the other hand, indicate a weak pressure gradient and light winds.
Pressure differences observed on the daily weather charts are caused by a number of factors. But the principal factor which creates these differences is the unequal heating of the earth’s land- sea surface.
In other words, temperature differences are responsible for generating a pressure gradient and thereby creating winds. Hence, there is a close relationship between pressure and temperature.
Thus, greater the temperature differences, steeper the pressure gradient and the resultant wind. Diurnal variation of temperature and the resultant pressure gradients are confined to a very shallow layer of the atmosphere.
But latitudinal variations in the amount of insolation received generate the atmospheric circulation on a much larger scale.
.jpg)
The Coriolis force produced by the rotation of the earth has its effect on every moving object, whether it is an ocean current or a bullet fired from the gun. Strictly speaking, Coriolis force is not a force in the true sense of the term.
In fact, it is an effect which results from the rotational movement of the earth and the movement of air relative to the earth. The Coriolis force is zero at the equator and maximum at the poles.
It acts at right angles to the horizontal direction of the wind, and it is directly proportional to its horizontal velocity. In the northern hemisphere the Coriolis force acts to the right of the direction of wind, and in the southern hemisphere it acts to the left.
That is why all winds in the northern hemisphere tend to move toward the right and those of the southern hemisphere to the left with respect to the rotating earth.
This accounts for the fact that in the northern hemisphere winds blow counter-clockwise around the centres of low pressure, but clockwise in the southern hemisphere.
The Coriolis force is directly proportional to: (a) horizontal velocity of the moving body; (b) mass of the moving body; and (c) sine of the latitude.
That is why this force, as stated earlier, is maximum at the poles where the plane of the deflective force is parallel to the earth’s surface, and is reduced to zero at the equator where there is no component of deflection in a plane parallel to the surface.
Since the Coriolis force acts at right angles to the horizontal direction of the moving object, it affects its direction and not the speed. Besides, this force is equal in all directions.
Geostrophic wind
.jpg)
When a wind, usually above a height of 600 meters, blows parallel to the isobars, it is called the geostrophic wind. Geostrophic wind has also been defined as the horizontal wind velocity in which the Coriolis force exactly balances the horizontal pressure force.
When the wind motion is almost in a straight line without friction force acting on it, it is worked upon only by two forces: the Coriolis force and the pressure gradient force. These forces are equal, and are directed at right angles to the wind.
It may be pointed out that these forces are opposed to each other. Under the influence of pressure gradient force, which always works at right angles to the isobars, the parcel of air begins to accelerate directly towards the area of low pressure.
But no sooner than the wind begins to blow, the Coriolis force deflects it to the right in northern hemisphere and to the left in the southern hemisphere.
Since the Coriolis force is proportional to wind speed, it intensifies with the acceleration. Ultimately, the wind is deflected to the extent that it starts blowing parallel to the isobars.
The pressure gradient force is directed towards the area of low pressure and is opposed by the Coriolis force. This latter force, as stated earlier, is directed towards the area of high pressure.
When the two opposing forces are equal in magnitude, the wind will continue to flow parallel to the isobars. However, the wind speed remains constant.
This is so because in this condition the pressure gradient flow, being oriented at right angles to the flow, does not cause any further acceleration; and the Coriolis force being proportional to the wind speed also remains constant.
Hence a balance is reached between these two opposing forces and is maintained further, so that the wind continues to flow parallel to the isobars.
These are, however, idealized conditions for which it is essential that the pressure gradient force must generate a wind with the exact velocity required to produce a Coriolis force equal to itself. But this seldom occurs nature.
In fact, the wind, instead of blowing parallel to the isobars, tends to adjust its speed and direction so as to reach a balance between the pressure gradient force and the Coriolis force.
The state of equilibrium reached by the two opposing forces is called geographic balance. Thus, geographic winds are those that are generated by this balance of the two opposing forces.
A steep gradient force will create winds with high velocities and these in turn will generate an equally strong Coriolis force.
It was Buys Ballot, a Dutch meteorologist, who in 1857 formulated this simple relationship between wind direction and pressure distribution. This is known as Buys Ballot’s law which states: “In the northern hemisphere, if you stand with your back to the wind, there will be low pressure to your left and high pressure to your right.
In the southern hemisphere, the Coriolis deflection being to the left, the situation is reversed.” It must be remembered that Buys Ballot’s law is applicable to the wind aloft.
In case of air flow near the earth’s surface, this law should be applied with some caution because of so many geographical factors which create local disturbances in the larger circulation.
Because of friction force and various other geographical factors, in the real atmosphere the winds are seldom purely geographic. However, the significance of a hypothetical geographic flow lies in the fact that this interrelationship between pressure and winds makes the upper-air weather charts more reliable by providing checks and balances.
Besides, it helps in describing the atmospheric conditions aloft with the least number of direct observations of the upper-air.
Help is taken from a number of scales to measure the geographic winds. Velocities of the geographic wind are measured from the isobars drawn on the Constant Level Charts or Constant Pressure Charts.
While constructing scales to measure the velocities of the geographic winds, the following facts are taken into consideration: (a) scale of the weather chart for which the geographic wind scales are to be used, (b) latitudinal extent, (c) spacing of isobars, (d) density of air, and (e) unit of the wind speed used.
As regards geographic wind speed, it should be remembered that it is (a) directly proportional to the pressure gradient, or, if the isobar pressure interval is taken to be constant, it is inversely proportional to the spacing of isobars: (b) inversely proportional to the sine of the latitude; (c) inversely proportional to air density.
Gradient wind:
.jpg)
A wind moving along the isobars at such a velocity that the force due to pressure gradient is balanced by the deflective and centrifugal effects is called a gradient wind.
In other words, gradient wind refers to the horizontal wind velocity in which balance is achieved between the Coriolis force, pressure force and centrifugal force.
In the figure, the three forces affecting a moving parcel of air and the resultant gradient wind around the high as well as low pressure centers in the northern hemisphere are shown.
Theoretically the pressure gradient force tends to move air in a straight line, but as soon as motion begins, the Coriolis force causes it to move in a curved path. If the motion of air is along the curved or circular isobars, centrifugal force is developed which tends to pull the air outward from the centre of curvature.
But the curved path of air is maintained by an inward acting force, i.e., the centripetal force. The centrifugal force is equal in magnitude and opposite in sign to the centripetal acceleration.
It may be pointed out that in the case of winds blowing in a curved path, as in a cyclone or an anticyclone; the geographic balance that is achieved in the case of geographic winds is not maintained.
It shows that for geographic gradient flow around a centre of the high pressure, the pressure gradient force is directed outward and is balanced by the inward-directed Coriolis force.
In the northern hemisphere where the Coriolis force deflects the wind motion to the right, the resultant wind blows clockwise about a high.
On the contrary, around a low-pressure centre the inward-directed pressure gradient force that is balanced by the outward- directed Coriolis force, results in anti- clockwise flow in the northern hemisphere.
Since Coriolis force deflects winds to the left in the southern hemisphere, the flow is clockwise around low-pressure centers and counter-clockwise around high-pressure centers.
Now, let us examine as to how the speed of cyclonic and anticyclonic flow is affected by the curvature of isobars. According to Newton’s first law of motion, whenever the flow is curved, there must necessarily be a force which will change its direction even when there is no change in speed.
As already explained, in a high-pressure centre the outward directed pressure gradient force is balanced by the inward-directed Coriolis force. But in order to maintain the curvature of the path (parallel to the isobars) the Coriolis force must be strong enough to balance the pressure gradient force and accelerate the air inward.
In other words, the Coriolis force must be greater than the pressure gradient force so as to overcome the air’s tendency to flow in a straight line. On the other hand, in a cyclonic flow the pressure gradient force must exceed the Coriolis force.
Since the magnitude of Coriolis force is proportional to wind speed, the result is that with equal pressure gradients the anticyclonic winds exceed cyclonic winds.
It is to be noted. The pressure gradient force and the Coriolis force both are in a state of imbalance, a fact that is essential to provide the change in direction required for a curved flow.
However, in the real atmosphere we experience strongest wind associated with low- pressure systems. This apparent paradox is resolved when we recall that the pressure gradients of cyclones are stronger than those of anticyclones.
The gradient wind, thus, is another approximation to the actual wind; it is similar to the geographic wind except only that the effect of the centrifugal force is involved.
The gradient wind may then be defined as the wind that corresponds to the balance between pressure forces on the one hand, the Coriolis force and centrifugal force, on the other.
At or near the earth’s surface friction is an important factor affecting wind. But its effect is confined to only a few thousand meters from the surface. Frictional forces act not only to slow the wind movement but also to change the wind direction.
Since Coriolis force is proportionate to wind speed, the friction consequently reduces it. On the contrary, the pressure gradient force remains unaffected by wind speed; hence it exceeds the Coriolis force along or near the earth’s surface.
This results in the movement of air at an angle across the isobars toward the low pressure area. Irregularities or roughness of the ground determine the angle at which the wind will cross the isobars while blowing from high to low pressure.
It also controls the speed of wind. Friction is relatively lower over the ocean surface. The angle at which wind drifts across the isobars over the relatively smooth ocean surface varies from 10 to 20 degrees, and the wind speeds are reduced to about two-thirds of the geotropic flow aloft.
Over the rough surface where frictional forces are much larger, winds cross the isobars at an angle of 45 degrees. Here the speed of wind may also be reduced by as much as 5 per cent.
As noted above, winds in the lowest layers of atmosphere are greatly influenced by the frictional force. It has also been noted that the effect of friction is to reduce the wind speed.
This frictional effect is distributed upward because of the viscosity of the air. There is an intermingling of different layers of the atmosphere with different wind velocities.
Thus, slow-moving wind in one layer mixes with fast-moving wind of an adjacent layer. It results in increasing the initially low speeds and in decreasing the initially high speeds.
The frictional effects are carried upward from the earth’s surface by the vertical movement of eddies. They transport slow- moving air from lower altitude to higher altitude, and fast-moving air from higher to lower altitudes.
At about 1000 meters from the ground, the effect of frictional forces becomes too small and, therefore, the winds are very nearly equal to the geostrophic wind.
The variation of wind with elevation through the friction layer is represented by an equi-angular spiral which is also called the Ekman Spiral.
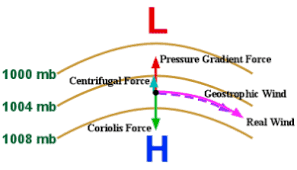For the centrifugal action of wind, see the portion of this chapter on gradient wind. However, it is worth remembering that centrifugal force is hardly a force in the true sense of the term.
It results from a state of imbalance existing between other forces when isobars are curved. In fact, this imbalance is necessary to provide the change in direction needed for curved flow.
The Coriolis force is a factor which operates forcefully only when there is a high velocity wind with a small radius of curvature as in small-sized violent tropical storms. Let us recall that it acts in a direction radically outward from the centre of oil curvature of the wind’s path.
© 2024 iasgyan. All right reserved